Schwingkreis
LC-Schwingkreis
Der Schwingkreis (LC-Schwingkreis) ist in der Hochfrequenztechnik eine wichtige Schaltung, bestehend aus Spule(Induktivität L) und Kondensator (Kapazität C).
Reihenschwingkreis:

Kreisfrequenz ω:
ω = Kreisfrequenz
π = Kreiszahl (2π = Bogenmaß von 360°)
f = Frequenz
T = Periodendauer
φ = Phasenwinkel
t = Zeit
L = Induktivität
C = Kapazität
Die Einheit der Kreisfrequenz [s-1] wird in pro Sekunde angeben und nicht wie bei der Frequenz [s-1] in Hertz.
Die Bedeutung des LC-Swingkreises in der Hochfrequenztechnik liegt darin, dass
beide Bauelemente Energie E speichern und später wieder freigeben können.
Fügt man der Schaltung von außen Energie E zu, z.B. durch das Aufladen des Kondensators (Kapazität C) oder der Spule(Induktivität L), pendelt die zugeführte Energie zwischen den beiden Baulementen hin und her.
Dadurch fungieren der Kondensator (Kapazität C) und Spule(Induktivität L) abwechselnd als Energiequelle und Energiespeicher.
Parallelschwingkreis:

Der Kondensator (Kapazität C) benötigt beim Ladevorgang elektrische Energie zum Aufbau eines elektrischen Feldes E:

Die Spule(Induktivität L) baut ein magnetisches Feld H auf:

Für die Veranschaulichung des elektrischen Feldes E bzw. magnetischen Feldes H dient die Darstellung der Feldlinien.
Pendelnde Energie E:
In einem LC-Schwingkreis ist die Energie eines geladenen Kondensators (Kapazität C) in Form des elektrischen Feldes E (elektrische Kapazität) gespeichert.
Der Kondensator (Kapazität C) entlädt sich im Schwingkreis über die Spule(Induktivität L), in der daraufhin ein magnetisches Feld H als Energiespeicher (Induktionsspannung) aufgebaut wird.
Sobald der Kondensator (Kapazität C) vollständig entladen ist, steckt die Energie im magnetischen Feld H der Spule(Induktivität L) und es fließt kein Strom I mehr.
Ohne Stromfluss bricht wiederum das Magnetfeld der Spule(Induktivität L) zusammen und die Induktionsspannung der Spule(Induktivität L) bewirkt einen Stromfluss, mit dem der Kondensator (Kapazität C) - diesmal umgekehrt polarisiert - geladen wird.
Gedämpfte & ungedämpfte Schwingung
Bei schwingfähigen Systemen werden gedämpfte und ungedämpfte Schwingungen unterschieden.
In einem theoretisch verlustfreien LC-Schwingkreis würde sich der Lade- und Entladevorgang zwischen Kondensator (Kapazität C) und Spule(Induktivität L) als ungedämpfte Schwingung unaufhörlich wiederholen.

Da in einer Schaltung aber Verluste auftreten (z.B. Wärmeverluste: ohmscher Widerstand R), klingt die Schwingung bei jedem Pendelvorgang allmählich ab.
Will man das Abklingen verhindern, also eine ungedämpfte Schwingung erreichen, muß man im richtigen Moment der Schwingung Energie zuführen.
Die Eigenkreisfrequenz ω0 oder Kennkreisfrequenz ω0 beschreibt das ungedämpfte System.
Die Kreisfrequenz ω beschreibt die gedämpfte Schwingung.
Zwischen der Kreisfrequenz ω und der Eigenkreisfrequenz ω0 besteht der folgende Zusammenhang:
ω = Kreisfrequenz [s-1]
ω0 = Eigenkreisfrequenz [s-1]
δ = Abklingkonstante [s-1]
Die Kreisfrequenz ω bleibt sowohl bei einer gedämpften als auch ungedämpften Schwingung während des gesamten Schwingungsvorgangs konstant.
Lediglich die Amplitude y der gedämpften Schwingung verringert sich mit zunehmender Schwingungsdauer.

Bei der ungedämpften Schwingung bleibt die Gesamtenergie des Systems erhalten. Das wird dadurch erreicht, dass einem Oszillator durch äußere Erregung eine Schwingung aufgezwungen wird.
Resonanzfrequenz f0:
Mit Resonanzfrequenz f0 (≙ Eigenfrequenz f0) wird die Frequenz f bezeichnet, in die sich ein schwingfähiges System nach einmaliger Anregung natürlich einschwingt.
Die Zeitdauer einer Pendelschwingung eines LC-Schwingkreises hängt von der Kapazität C und der Induktivität L ab.
Für große Kapazitäten C und Induktivitäten L ist die Frequenz f der Schwingung sehr niedrig, da die Lade- und Entladevorgänge sehr lange dauern.
Berechnung der Resonanzfrequenz (Thomsonsche Schwingkreisformel):
f0 = Resonanzfrequenz [Hz]
π = Kreiszahl (Pi) [1]
L = Induktivität [H]
C = Kapazität [F]
Daraus folgt, dass die Resonanzfrequenz f0 umgekehrt proprotional zur Induktivität L und Kapazität C ist.
Theoretischer Übergang einer Monopol-, bzw. Dipol-Antenne aus einem LC-Schwingkreis:
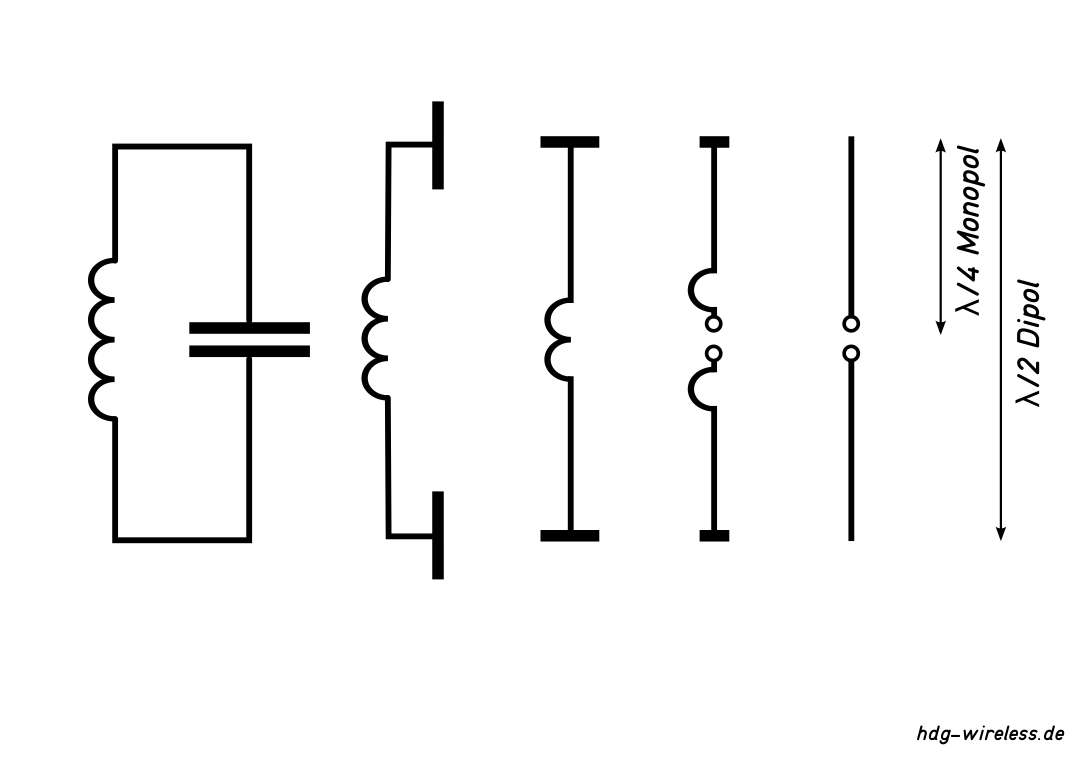
Die Eigenfrequenz f0 (≙ Resonanzfrequenz f0) des LC-Schwingkreises wird umso größer, je kleiner die Fläche A der Kondensatorplatten und die Windungszahl N der Spule werden.
Am Ende dieser Reduzierung entsteht ein möglichst dünner Metalldraht, in dem ein hochfrequenter Wechselstrom ≂ möglich ist.
Bei dem so geöffneten Schwingkreis haben die elektrischen und magnetischen Feldlinien eine weite Ausdehnung in den umgebenden Raum hinein.