rf-management & monitoring rental Mikrofone [drahtlos] Mikrofone [kabelgebunden] In-Ear-Monitoring Betriebsfunkgeräte Veranstaltungstechnik Ersatzteile [Verkauf] referenzen kontakt glossar impressum
Mikrofone [drahtlos] Mikrofone [kabelgebunden] In-Ear-Monitoring Betriebsfunkgeräte Veranstaltungstechnik Ersatzteile [Verkauf]


hdg-wireless | glossary

[befindet sich noch im Aufbau... kann und wird 'noch' Fehler und Fehlfunktionen enthalten! Start 07.2023, Stand: 12.2025]

Inhalt

0 · 1 · 3 · 5 · 6
A · B · C · D · E · F · G · H · I · J · K · L · M · N · O · P · Q · R · S · T · U · V · W · Z

Abklingkonstante δ

Dämpfungskonstante

Die Abklingkonstante δ ist das Produkt aus Kennkreisfrequenz ω0 und Dämpfungsgrad D.

Abklingkonstante δ:

δ = ω0D     [s-1]
(für |D| < 1 )

δ = Abklingkonstante [s-1]
ω0 = Kennkreisfrequenz [s-1]
D = Dämpfungsgrad [1]

Im Zeitverlauf einer linearen Schwingung kann sich die Amplitude y einer Schwingung verändern. Die Abklingkonstante δ gibt Aufschluß darüber, in welche Richtung die Änderung erfolgt:

Bei positiver Abklingkonstante δ klingt die Schwingung ab.

Schwingung mit unterschiedlichen Abklingkonstanten

Bei negativer Abklingkonstante δ nimmt die Amplitude y der Schwingung exponentiell zu.

Amplitude y (gedämpft):

y(t) = ŷ sin(ωt+φ0) e-δt     [tba.]

y = Amplitude [tba.]
t = Zeit [s]
ŷ = Amplituden-Scheitelwert [tba.]
ω = Kreisfrequenz [s-1]
φ0 = Nullphasenwinkel [rad]
e = e-Funktion [1]
δ = Abklingkonstante [s-1]

Beschreibt den Zeitverlauf einer linearen, gedämpften Schwingung.

Amplitude: Zeitverlauf einer linearen, gedämpften Schwingung.

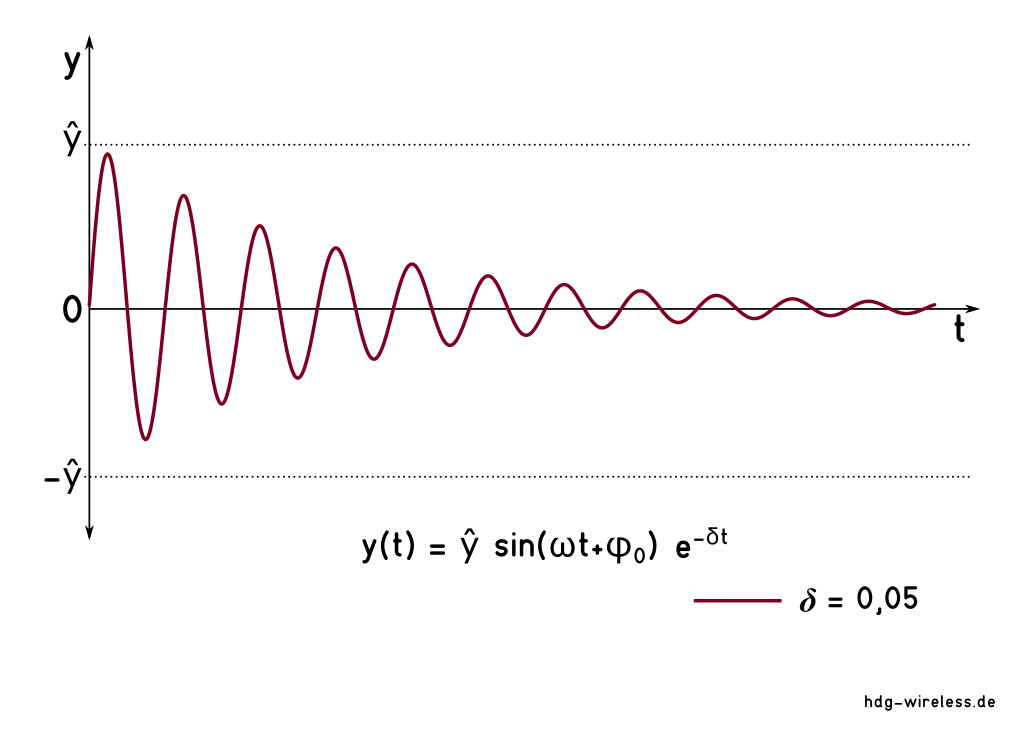
Bei einer gedämpften Schwingung (δ > 0) ist die Amplitude y nach t = 3/δ s auf unter 5 % der Ausgangsamplitude abgeklungen.

t =
3 / δ
    [ s ]

Für eine Abklingkonstante δ = 0,05 s-1 bedeutet das, dass die Amplitude y der Schwingung nach 60 Sekunden um über 95 % abgenommen hat.

⇒ Amplitude
⇒ Dämpfungsmaß [ ⇒Dämpfungsgrad ]
⇒ Dämpfungsmaß
⇒ Eigenkreisfrequenz
Formelsammlung
⇒ Kennkreisfrequenz
⇒ Kreisfrequenz
⇒ Schwingung

    top  

Quellen

A
⇒  Abgleichen der Rauschsperre an der UKW Funkanlage. simrad-yachting.com
⇒  Abklingkonstante. wikipedia.org
⇒  Abschlußwiderstand. vigedo.de
⇒  Abstand zweier Punkte. studyflix.de
⇒  Angular frequency and frequency. lambdageeks.com
⇒  ANP109 | Impedanzspektren unterschiedlicher Kondensatortechnologien. we-online.com
⇒  Anpassung mit Stichleitungen unter Berücksichtigung der Verluste. dl2fbo.de
⇒  Anpassungsd%C3%A4mpfung. wikipedia.org
⇒  Antenne. wikipedia.org
⇒  Antenne. uni-rostock.de
⇒  Antennen und Wellenausbreitung. ethz.ch
⇒  Antennen-Theorie. mergerandfriends.de
⇒  Antennendiagramm. wikipedia.org
⇒  Antennengewinn. wikipedia.org
⇒  Antennenpraktikum. ethz.ch
⇒  Antennenwirkflaeche | Hochfrequenztechnik. youtube.com (BrainGain)
⇒  Arbeit (Physik). wikipedia.org
⇒  Atmosphä,;rische_Störungen. wikipedia.org
⇒  Ausbreitungsgeschwindigkeit. simpleclub.com
B
⇒  Bauelemente-Reflexionsfaktor. funkamateur.de
⇒  Bel (Einheit). wikipedia.org
⇒  Bezugspegel_(Tontechnik). wikiwand.com
⇒  Blindwiderstand. elektrotechnik-fachwissen.de
⇒  Boltzmann-Konstante. wikipedia.org
C
⇒  Coulombsches Gesetz. wikipedia.org
D
⇒  Dämpfung. wikipedia.org
⇒  Dämpfungsfaktor. wikipedia.org
⇒  Dämpfungsgrad. wikipedia.org
⇒  DARC-Online-Lehrgang Technik Klasse A Kapitel 13: Frequenzaufbereitung. darc.de
⇒  Das Dezibel. elektroniktutor.de
⇒  Der Crest-Faktor bei DVB-T-(OFDM-) Sendeanlagen und seine Auswirkung auf die Dimensionierung der Leistungskomponenten. rohde-schwarz.com
⇒  Der Hauteffekt. Der Skin­Effekt, seine Auswirkungen auf den Gewinn, den Verlust und die Resonanzfrequenz in KW­-Antennen­-Systemen. dl2fbo.de
⇒  Der Innenwiderstand. medienportal.siemens-stiftung.org
⇒  Der Wirkungsgrad von Antennen. dl9ah.de
⇒  Dezibel, Dämpfung, Kabel. darc.de
⇒  Die geheimnisvolle 50-Ohm-Impedanz: Woher sie kommt und warum wir sie verwenden. altium.com
⇒  Die komplexen Zahlen. frankfurt-university.de
⇒  Die wichtigsten Antennenkennwerte im Überblick. beam-verlag.de
⇒  Dielektrizitätskonstante. studyflix.de
⇒  Dipol. dl1glh.de
⇒  Dipolantenne. wikipedia.org
⇒  Dispersion (Physik). wikipedia.org
E
⇒  e-Funktion. studyflix.de
⇒  Effektivwert. wikipedia.org
⇒  Eigenschaften und Dimensionierung von Koaxialkabeln, Streifenleitungen, Finleitungen, Richtkopplern und Hochfrequenzfiltern. bilder.buecher.de
⇒  Ein Leitfaden für Antennen und Koaxialantennen-Stecker und Kabel. distrelec.com
⇒  Einheitskreis. wikipedia.org
⇒  Einige Ergebnisse der Leitungstheorie. lntwww.de
⇒  Elektrische Feldkonstante. wikipedia.org
⇒  Elektrische Feldstärke. wikipedia.org
⇒  Elektrische Flussdichte. wikipedia.org
⇒  Elektrische Flussdichte. maths2mind.com
⇒  Elektrische Flussdichte & Elektrischer Fluss | Physik Tutorial. youtube.com
⇒  Elektrische Impedanz. wikipedia.org
⇒  Elektrische Kapazität. wikipedia.org
⇒  Elektrische Ladung. serlo.org
⇒  Elektrische Netze Folge 3.4: Leitungen - Wellenwiderstand und stehende Wellen. youtube.com (E. Waffenschmidt)
⇒  Elektrische Spannung. studyflix.de
⇒  Elektrischer Strom. studyflix.de
⇒  Elektrischer Widerstand. wikipedia.org
⇒  Elektrisches Feld. wikipedia.org
⇒  Elektromagnetische Felder. studysmarter.de
⇒  Elektromagnetische Felder. stmuv.bayern.de
⇒  Elektronik Vorlesung. physik.uni-greifswald.de
⇒  Elementarladung. wikipedia.org
⇒  Erdungswiderstand. wikipedia.org
⇒  Erläuterung der Bewertungsverfahren nach BEMFV. bundesnetzagentur.de
⇒  Erzwungene Schwingungen. tu-dresden.de
⇒  Eulersche Zahl. wikipedia.org
F
⇒  Faktor. dwds.de
⇒  Felder in der Physik. youtube.com
⇒  Feldstärke und Durchflutungsgesetz. ingenieurkurse.de
⇒  Feldwellenwiderstand. brockhaus.de - Enzyklopädie
⇒  Feldwellenwiderstand. universal_lexikon.de-academic.com
⇒  Feldwellenwiderstand. buergerwelle.de
⇒  Fern- und Nahfeld. solconia.de
⇒  Flächenwiderstand. wikipedia.org
⇒  Formelsammlung für Leitungstheorie. tu-braunschweig.de
⇒  Formelsammlung für die Funkamateurprüfung. afu-blindenausbildung.a36.de
⇒  Freiraumdämpfung. wikipedia.org
⇒  Freiraumdämpfung. radartutorial.eu
⇒  Frequenz. wikipedia.org
⇒  Frequenz- und Wellenbereiche. radartutorial.eu
⇒  Frequenz, Amplitude, Schwingungen: Wie entsteht Resonanz. blog.ringfeder.com
G
⇒  Galaktisches Rauschen. demvt.de
⇒  Grad Celsius. wikipedia.org
⇒  Grundlagen der Antennentheorie. funkfrequenzen01.de
⇒  Grundlagen zur Elektrotechnik. thm.de
H
⇒  Halbwertsbreite. wikipedia.org
⇒  Halbwertsbreite. 50ohm.de
⇒  Heinrich Hertz: Nachweis elektromagnetischer Wellen. dieter-heidorn.de
⇒  Hilfsmittel. bundesnetzagentur.de
I
⇒  Imaginaere Einheit. maths2mind.com
⇒  Impedanz. studyflix.de
⇒  Impedanz-Scheinwiderstand. computerweekly.com
⇒  Induktion. emf.ethz.ch
⇒  Induktion Grundlagen (+ Herleitung). Physik - simpleclub
⇒  Induktivität. studysmarter.de
⇒  Innenwiderstand der Batterie. wanroy.de
⇒  Isolator. studysmarter.de
⇒  Isotropstrahler. wikipedia.org
J
K
⇒  Kelvin. wikipedia.org
⇒  Koaxial Kabel - Aufbau und Verwendung. elspecgroup.de
⇒  Koaxkabel. dl4zao.de
⇒  Komplexe Zahlen. massmatics.de
⇒  Komplexer Widerstand Z. maths2mind.com
⇒  Koordinatensystem. lernort-mint.de
⇒  Kraft Physik. studyflix.de
⇒  Kreiswellenzahl. rhetos.de
⇒  Kreiszahl. wikipedia.org
⇒  Kreiszahl. 3.1415926[...].eu
L
⇒  Ladungsdichte. wikipedia.org
⇒  Leistungsdichte (Feldstärke). radartutorial.eu
⇒  Leistungsflussdichte. bfs.de
⇒  Leistungsgröße. wikipedia.org
⇒  Leitfähigkeit. wikipedia.org
⇒  Leitung. elektroniktutor.de
⇒  Leitungsbeläge. wikipedia.org
⇒  Leitungstechnik. radartutorial.eu
⇒  Leitungswiderstand, Widerstand eines Leiters. xplore-dna.net
⇒  Lichtgeschwindigkeit. wikipedia.org
⇒  Logarithmus. wikipedia.org
⇒  Lorentzkraft. wikipedia.org
⇒  Lorentzkraft. studyflix.de
M
⇒  Magnetische Feldstärke im Leiter. technikermathe.de
⇒  Magnetische Flussdichte. studysmarter.de
⇒  Magnetische Permeabilität. wikipedia.org
⇒  Magnetische_Feldstärke. wikipedia.org
⇒  Magnetischer Fluss und Induktionsgesetz. leifiphysik.de
⇒  Magnetisches Feld. studyflix.de
⇒  Magnetisches Feld. lernhelfer.de
⇒  Messungen an Leistungsendstufen. do8ail.bplaced.net
⇒  Mikrofonpegel und ihre Bezugswerte. sengpielaudio.com
⇒  Minimale Dämpfung bei Koaxialkabel. elspecgroup.de
N
⇒  Nahfeld. chemie.de
⇒  Nahfeld und Fernfeld (Antennen). wikipedia.org
⇒  Nahfeld und Fernfeld (Antennen). cosmos-indirekt.de
⇒  Nahfeld/Fernfeld. radartutorial.eu
⇒  Nennpegel. adt-audio.de
⇒  Nichtleiter. wikipedia.org
⇒  Numerische Simulation elektrothermischer Prozesse. tu-darmstadt.de
O
P
⇒  Pegel. wikipedia.org
⇒  Pegel. spektrum.de
⇒  Pegel-Skin-Leitungen. techniker.pi-pro.de
⇒  Pegelrechnung. sengpielaudio.com
⇒  Permeabilitäszahl. chemie.de
⇒  Permeabilität. asa-trafo-bau.de
⇒  Permeabilität (Magnetismus). chemie.de
⇒  Permittivität. wikipedia.org
⇒  Phasenverschiebung. wikipedia.org
⇒  Phasenwinkel. wikipedia.org
⇒  photon. studyflix.de
⇒  Photonen. uni-paderborn.de
⇒  Polarisation. wikipedia.org
⇒  Poynting Vektor und Energietransport in elektromagnetischen Feldern. Rene Matzdorf
⇒  Poynting-Vektor. cosmos-indirekt.de
⇒  Punktladung. wikipedia.org
Q
⇒  Quant. wiktionary.org
⇒  Quantenmechanik. studysmarter.de
R
⇒  Rückflussdaempfung - Reflexionen auf der Datenstrecke. itnetworks.softing.com
⇒  Raumwinkel. wikipedia.org
⇒  Raumwinkel. schorsch.com
⇒  Rauschen. physik.uni-ulm.de
⇒  Rauschen. radartutorial.eu
⇒  Rauschen. meister-automation.de
⇒  Rauschpegel. lte-anbieter.info
⇒  Rauschsperre. wikipedia.org
⇒  Rechner Sensitivity. sengpielaudio.com
⇒  Reflexion. Stehwellen.. uni-muenster.de
⇒  Relativer Pegel (dB) / Absoluter Pegel (dBmW). youtube.com
⇒  Resonanz. wikipedia.org
⇒  Resonanzfrequenz. wikipedia.org
⇒  Resonator. wikipedia.org
⇒  Richtcharakteristik. wikipedia.org
S
⇒  S-Meter - Rauschen - Empfindlichkeit. dl4zao.de
⇒  Satellitenempfang. media.elv.com
⇒  Schalldruckpegel. wikipedia.org
⇒  Scheinwiderstand. elektrotechnik-fachwissen.de
⇒  Schirmd&aiml;mpfung. wikipedia.org
⇒  Siemens (Einheit). wikipedia.org
⇒  Signalverlust zwischen Antenne und Empfänger. circuitdesign.de
⇒  Skin-Effekt. wikipedia.org
⇒  Skin-Effekt. elektronik-kompendium.de
⇒  Skin-Effekt. radartutorial.eu
⇒  Skin-Effekt. academic.com
⇒  Skin-Effekt. dl2fbo.de
⇒  Skin-Tiefe. academic.com
⇒  Spannungsanpassung. wikipedia.org
⇒  Spannungsanpassung (Rechner). sengpielaudio.com
⇒  Stabantenne (GP)- Funktion und Eigenschaften. docplayer.org
⇒  Stehende Welle. wikipedia.org
⇒  Stehende Welle. studyflix.de
⇒  Stehende Wellen - Einführung. leifiphysik.de
⇒  Stehwellenverhältnis. wikipedia.org
⇒  Strahlenarten. thm.de
⇒  Strahlstärke. wikipedia.org
⇒  Strahlungsleistung. wikipedia.org
⇒  Stromanpassung. wikipedia.org
⇒  Stromquelle (Schaltungstheorie). wikipedia.org
⇒  SWR. darc.de
T
⇒  Theorie der Leitungen. mikrocontroller.net
⇒  Theoriea (Quantenmechanik). physik.uni-hamburg.de
⇒  There’s Nothing Magic About 50 Ohms. highfrequencyelectronics.com
⇒  Thomsonsche Schwingungsgleichung. wikipedia.org
⇒  Transferimpedanz. wikipedia.org
⇒  Transformator. wikipedia.org
U
V
⇒  Vektorielle Größen. lernhelfer.de
⇒  Vektorielle_Größe. wikipedia.org
⇒  Verkürzungsfaktor. hb9f.ch
⇒  Verlustfaktor. wikipedia.org
⇒  Verlustwinkel. wikipedia.org
⇒  Verschiebungsstrom. youtube.com - Rene Matzdorf
⇒  VHF-Monopolantenne des DLR-Satelliten BIROS. elib.dlr.de
⇒  Vollwinkel. wikipedia.org
⇒  Vor-/Rückverhältnis. 50ohm.de
W
⇒  Wanderwelle. wikipedia.org
⇒  Wann sind die dielektrischen Verluste des Koaxialkabels dominant?. elspec group
⇒  Was bedeutet Empfindlichkeit bzw. Übertragungsfaktor. neumann.com
⇒  Was ist die Wellenzahl und Kreiswellenzahl?. universaldenker.org
⇒  Was ist ein Zirkulator?. youtube.com
⇒  Was ist Rauschen. beam-verlag.de
⇒  Was ist Squelch in einem Radio. herdaradio.com
⇒  Was sind Quanten. ds.mpg.de
⇒  Welle-Teilchen-Dualismus. wikipedia.org
⇒  Welle-Teilchen-Dualismus. uni-tuebingen.de
⇒  Wellen. uni-leipzig.de
⇒  Wellenwiderstand. wikipedia.org
⇒  Wellenwiderstand. spektrum.de
⇒  Wellenwiderstand. elektronik-kompendium.de
⇒  Wellenwiderstand des Vakuums. wikipedia.org
⇒  Wieseo 6 dBu. adt-audio.de
⇒  Winkel. serlo.org
⇒  Winkelmaß. wikipedia.org
⇒  Wirkleistung. wikipedia.org
⇒  Worin unterscheiden sich Line-Level und Mic-Level?. shure.com
X
Y
Z
⇒  Zeitmaß (Winkel). wikipedia.org
⇒  Zirkulator. wikipedia.org