Skin-Effekt
Der Skin-Effekt beschreibt die frequenzabhängige, exponentielle Abnahme der Eindringtiefe einer elektromagnetischen Welle in die Oberfläche eines elektrischen Leiters und die damit verbundene konzentrische Verdrängung der Stromdichte über den Querschnitt des Leiters bei hochfrequenten Wechselströmen, vom Mittelpunkt hin zum Randbereich (Skin).
Skin-Effekt (vektorielle Stromdichte J→):
J→ = vektorielle Stromdichte [tba.]
J→0 = vektorielle Stromdichte bei Gleichstrom [tba.]
e = Eulersche Zahl [1]
d = Abstand vom Rand [m]
k = Dämpfungsfaktor (Stromeindringtiefe) [m-1]
Skin-Effekt:

Beim Skin-Effekt findet der Stromfluss mit zunehmender Frequenz f des Wechselstroms ≂ in einer immer dünner werdenden Schicht an der Oberfläche (Skin) des Leiters statt.
Die Stromdichte im Inneren des Leiters ist bei Gleichstrom gleichmäßig über den Querschnitt eines Leiters verteilt.

Bei Wechselstrom nimmt die Stromdichte exponentiell mit dem Abstand von der Oberfläche ab, bzw. die äquivalente Leitschichtdicke (Skin-Tiefe, Stromeindringtiefe) verringert sich.
Ursächlich für den Skin-Effekt werden vielfach eine dämpfende Wirkung (Dämpfungsfaktor k) auf die Eindringtiefe einer elektromagnetischen Welle in einen Leiter beschrieben oder die stromverdrängende Wirkung des durch Stromfluss im Leiter entstehenden Magnetfeldes und den ständigen Polaritätswechsel des Wechselstroms (magnetische Feldstärke H).

Das magnetische Wechsel-Feld soll dem Stromfluss in Achsennähe des Leiters einen zunehmenden Widerstand entgegensetzen.
Die äquivalente Leitschichtdicke δ ist der Abstand vom Rand des Leiters zu der Stelle des Leiterquerschnitts, an dem durch den Skin-Effekt die Feldstärke einer elektromagnetischen Welle um den Faktor 1/e (36,79 %) abgenommen hat, und stellt somit die Dicke (Skin-Tiefe) der äquivalent elektrisch leitenden Kreisringfläche A⊚ (äquivalente Fläche A) des Leiters bei hochfrequentem Wechselstrom dar.
Leitschichtdicke δ (Skin-Tiefe):
δ = Leitschichtdicke [m]
k = Dämpfungsfaktor (Stromeindringtiefe) [m-1]
R = Radius (Radius Leiter) [m]
r = Radius (Radius bis Leitschichtdicke) [m]
ρ = spezifischer Widerstand [Ωm]
ω = Kreisfrequenz [s-1]
µ = Permeabilität [Hm-1]
µ0 = Magnetische Feldkonstante [NA-2]
µr = Relative Permeabilität [1]
π = Kreiszahl (Pi) [1]
f = Frequenz [Hz]
σ = elektrische Leitfähigkeit [Sm-1]
Die Gleichung zur Berechnung der Leitschichtdicke δ zeigt die Abhängigkeit von der Signal-Frequenz f und den Einfluss der Materialeigenschaften elektrische Leitfähigkeit σ und Permeabilitätszahl µr (≙ relative Permeabilität µr) auf den Skineffekt:
Leitschichtdicke δ / Frequenz f
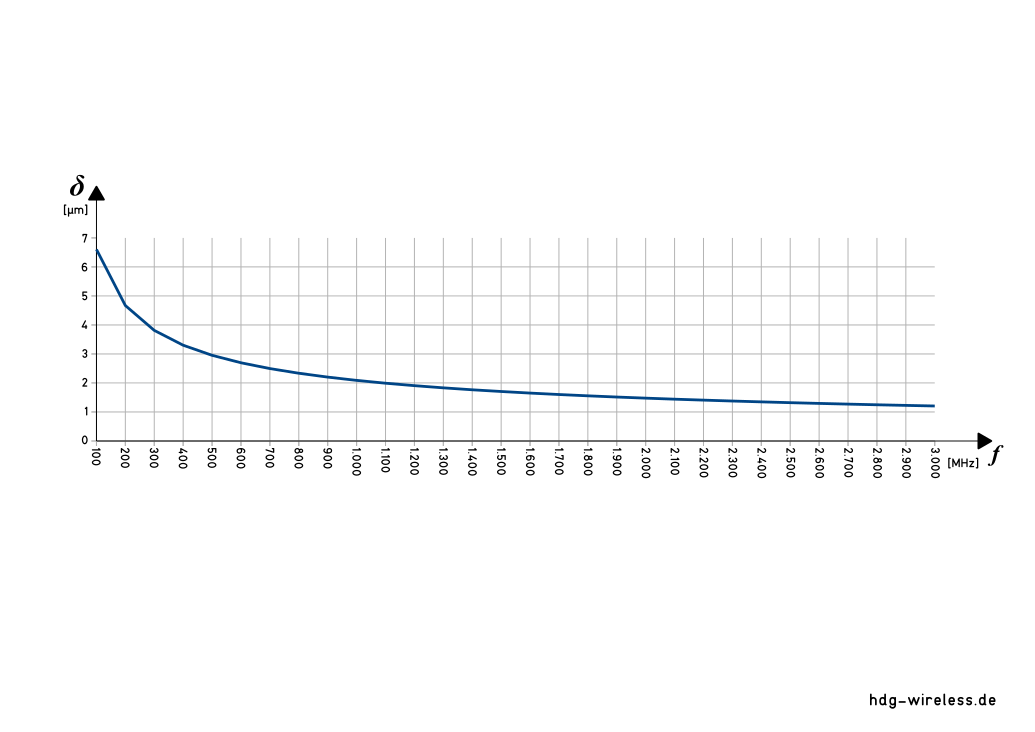
δ = Leitschichtdicke [m]
f = Frequenz [Hz]
µ0 = Magnetische Feldkonstante: 1,25664 · 10-6 [NA-2]
µr = Relative Permeabilität(Cu): 0,9999936 [1]
π = Kreiszahl (Pi) [1]
σ = elektrische Leitfähigkeit(Cu): 58,10575246949 [Sm-1]
Die Skin-Tiefe (≙ Leitschichtdicke δ) im Leiter nimmt ab, je größer die jeweiligen Werte (bzw. deren Produkt: f·µr·σ) werden.
|
Permeabilitätszahl µr und Permeabilität µ einiger Materialien |
||
| Medium | µr [1] |
µ [Hm-1] |
|---|---|---|
| Supraleiter | 0 | 0 |
| Blei, Zinn | tba. | tba. |
| Kupfer |
0,9999936 (1 - 6,4·10-6) |
1,256629·10-6 |
| Vakuum | 1 | 1,256637·10-6 |
| Luft |
1,0000004 (1 + 4·10−7) |
1,256638·10-6 |
| Eisen | 300 bis 10.000 |
0,000377
bis 0,012566 |
|
Spezifischer Widerstand ρ und elektrische Leitfähigkeit σ einiger Materialien: |
||
| Material |
ρ
[
Ω·mm2
m
]
|
σ [
m
Ω·mm2
]
|
|---|---|---|
| Cu (Kupfer, rein) | 0,01721 | 58,10575 |
| Ag (Silber) | 0,01500 | 66,66667 |
| Sn (Zinn) | 0,10000 | 10,00000 |
|
Für elektrische Leiter mit geringer Querschnittsfläche A wird der spezifische Widerstand ρ statt in der SI-Einheit (Ωm) in einer für dünne Drähte anschaulicheren Einheit angegeben.
ρ
[ Ωm ] ⇒
[
Ω mm2
m
]
|
||
Skin-Effekt: Litze vs. Volldraht
Die Verwendung von Litzen anstelle eines Volldrahts vergrößert die Oberfläche eines Leiters und dessen stromdurchflossene Kreisringfläche A⊚ in Abhängigkeit von dem Durchmesser d und der Leitschichtdicke δ.
A⊚ = Kreisringfläche [m2]
π = Kreiszahl (Pi) [1]
r = Radius [m]
δ = Leitschichtdicke [m]
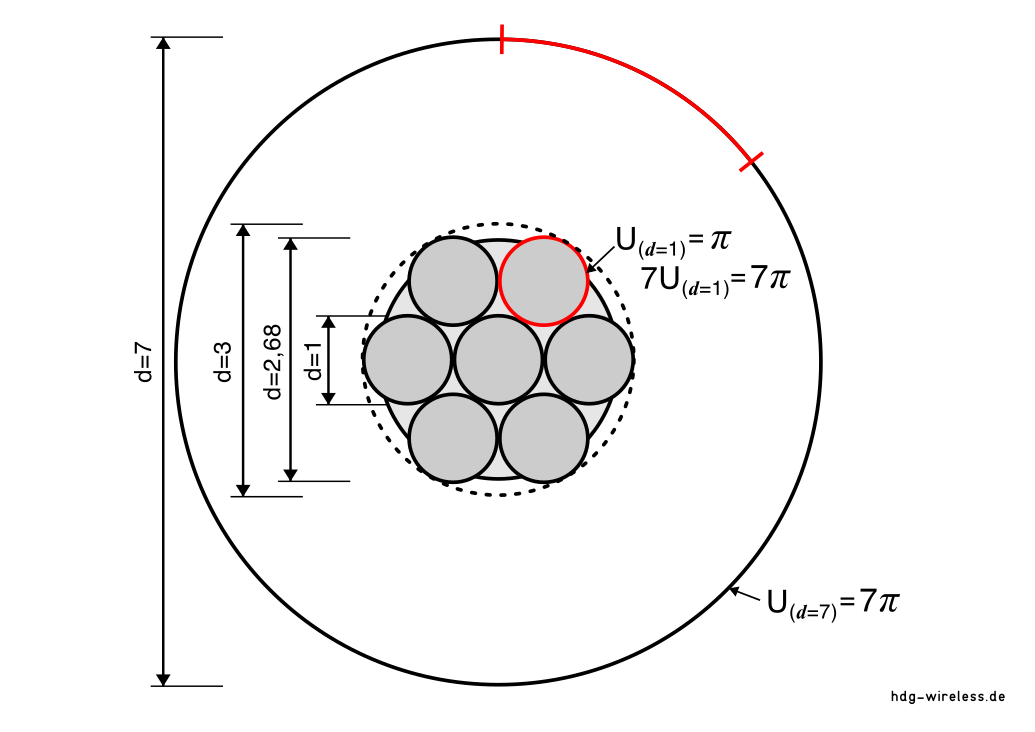
Für einen Leiter, bestehend aus 7 Litzen (dLitze = 1mm ⇒ ULitze = π), ergibt das einen Gesamtumfang aller Litzen von 7π [mm].
U = Kreisumfang [m]
r = Radius [m]
d = Durchmesser [m]
π = Kreiszahl (Pi) [1]
Ein Volldraht mit einem Umfang von 7π [mm] hat wiederum einen Durchmesser d von 7 mm, d.h. durch die Verwendung von Litzen anstelle eines Volldrahtes lässt sich mit geringerem Materialaufwand und kleinerem Kabeldurchmesser mehr Oberfläche erreichen und somit eine größere stromdurchflossene Leitschicht (Kreisringfläche A⊚) realisieren.
Dadurch reduziert sich auch der Skin-Effekt.
| Frequenz | Leitschichtdicke | Kreisringfläche A⊚ |
Ohmscher Widerstand R |
|
|---|---|---|---|---|
| f | δ | (Leiter: ∅ 1mm, Länge: 1m) | ||
|
π(R2-r2)
=
π(2r-δ)δ |
2πrδ | |||
| 1 Hz | 66,03 mm | 0,78540 mm2 | --- | --- |
| 10 Hz | 20,88 mm | 0,78540 mm2 | --- | --- |
| 20 Hz | 14,76 mm | 0,78540 mm2 | --- | --- |
| 50 Hz | 9,34 mm | 0,78540 mm2 | --- | --- |
| 100 Hz | 6,60 mm | 0,78540 mm2 | --- | --- |
| 200 Hz | 4,67 mm | 0,78540 mm2 | --- | --- |
| 500 Hz | 2,95 mm | 0,78540 mm2 | --- | --- |
| 1 kHz | 2,088 mm | 0,78540 mm2 | --- | --- |
| 2 kHz | 1,476 mm | 0,78540 mm2 | --- | --- |
| 5 kHz | 0,934 mm | 0,78540 mm2 | --- | --- |
| 10 kHz | 0,660 mm | 0,78540 mm2 | --- | --- |
| 20 kHz | 0,467 mm | 0,78195 mm2 | --- | 0,01173 Ω |
| 50 kHz | 0,295 mm | 0,65373 mm2 | --- | 0,01855 Ω |
| 100 kHz | 0,209 mm | 0,51898 mm2 | --- | 0,02624 Ω |
| 200 kHz | 0,148 mm | 0,39534 mm2 | --- | 0,03711 Ω |
| 500 kHz | 0,093 mm | 0,26595 mm2 | --- | 0,05867 Ω |
| 1 MHz | 66,03 µm | 0,19373 mm2 | 0,20743 mm2 | 0,08297 Ω |
| 2 MHz | 46,69 µm | 0,13982 mm2 | 0,14667 mm2 | 0,11734 Ω |
| 5 MHz | 29,53 µm | 0,09002 mm2 | 0,09276 mm2 | 0,18553 Ω |
| 10 MHz | 20,88 µm | 0,06422 mm2 | 0,06559 mm2 | 0,26237 Ω |
| 20 MHz | 14,76 µm | 0,04570 mm2 | 0,04638 mm2 | 0,37105 Ω |
| 50 MHz | 9,34 µm | 0,02906 mm2 | 0,02933 mm2 | 0,58668 Ω |
| 100 MHz | 6,60 µm | 0,02061 mm2 | 0,02074 mm2 | 0,8297 Ω |
| 200 MHz | 4,67 µm | 0,01460 mm2 | 0,01467 mm2 | 1,17337 Ω |
| 400 MHz | 3,30 µm | 0,01034 mm2 | 0,01037 mm2 | 1,65939 Ω |
| 500 MHz | 2,95 µm | 0,00925 mm2 | 0,00928 mm2 | 1,85526 Ω |
| 800 MHz | 2,33 µm | 0,00732 mm2 | 0,00733 mm2 | 2,34673 Ω |
| 1 GHz | 2,09 µm | 0,00655 mm2 | 0,00656 mm2 | 2,62373 Ω |
| 1.8 GHz | 1,56 µm | 0,00488 mm2 | 0,00489 mm2 | 3,5201 Ω |
| 2.4 GHz | 1,35 µm | 0,00423 mm2 | 0,00423 mm2 | 4,06466 Ω |
|
f = Frequenz [Hz] |
||||
⇒ Elektrische Ladung
⇒ Kupferverluste
⇒ Leitschichtdicke
⇒ Strom
⇒ Stromeindringtiefe [ ⇒Leitschichtdicke ]
⇒ Stromeindringtiefe [ ⇒Dämpfungsfaktor Eindringtiefe ]