Schwingung
Mit Schwingung wird die zeitliche Veränderung einer physikalischen Zustandsgröße um einem Mittelwert bezeichnet.
Schwingungen können nach zahlreichen Kriterien unterschieden werden.
Auf den Seiten hier sind im wesentlichen nur periodische und harmonische Schwingungen interessant. Diese können gedämpft und ungedämpft betrachtet werden.
Weitere Eigenschaften werden hier nicht weiter verfolgt.
Pendelnde Energie E:
In einem LC-Schwingkreis ist die Energie eines geladenen Kondensators (Kapazität C) in Form des elektrischen Feldes E (elektrische Kapazität) gespeichert.
Der Kondensator (Kapazität C) entlädt sich im Schwingkreis über die Spule(Induktivität L), in der daraufhin ein magnetisches Feld H als Energiespeicher (Induktionsspannung) aufgebaut wird.
Sobald der Kondensator (Kapazität C) vollständig entladen ist, steckt die Energie im magnetischen Feld H der Spule(Induktivität L) und es fließt kein Strom I mehr.
Ohne Stromfluss bricht wiederum das Magnetfeld der Spule(Induktivität L) zusammen und die Induktionsspannung der Spule(Induktivität L) bewirkt einen Stromfluss, mit dem der Kondensator (Kapazität C) - diesmal umgekehrt polarisiert - geladen wird.
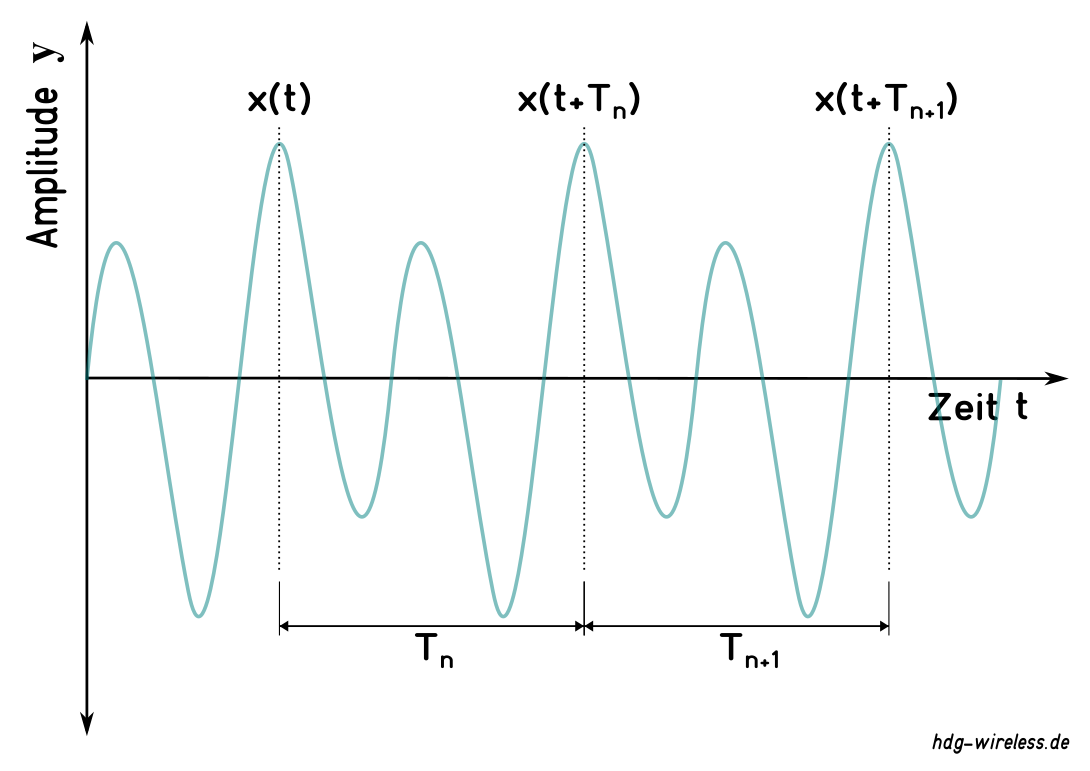
Periodische Schwingung
Wenn physikalische Zustandsgrößen x einer Schwingung in regelmäßigen Zeitabständen (Zeit t) wiederholt eintreten, wird von einer periodischen Schwingung (Periodendauer T) gesprochen:
x = Zustandsgröße
t = Zeit
x(t) = Zustandsgröße x zum Zeitpunkt t
n = Natürliche Zahl
T = Periodendauer
Periodendauer T:
T = Periodendauer
π = Kreiszahl
ω = Kreisfrequenz
f = Frequenz
Die Periodendauer T ist der Quotient aus einer vollständigen Schwingung von 360° (≙ 2π, dem vollen Bogenmaß arc(α)) und der Geschwindigkeit v des Schwingungsvorgangs in Form der Kreisfrequenz ω.
Die Frequenz f ist als Kehrwert der Periodendauer T definiert.
f = Frequenz [Hz]
T = Periodendauer [s]
c = Ausbreitungsgeschwindigkeit [ms-1]
c0 = Lichtgeschwindigkeit im freien Raum [ms-1]
ω = Kreisfrequenz [s-1]
π = Kreiszahl (Pi) [1]
Entsprechend läßt sich die Periodendauer T als Kehrwert der Frequenz f ermitteln.
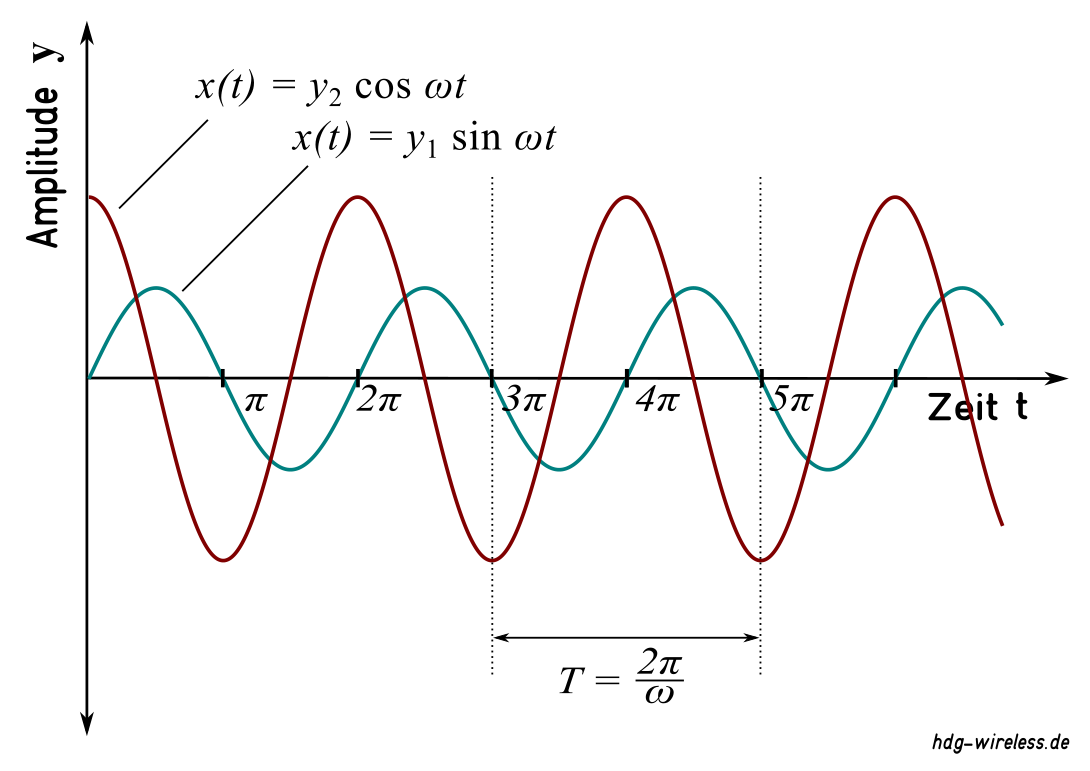
Harmonische Schwingung
Mit einer harmonischen Schwingung wird eine periodische Schwingung mit sinusförmigem Amplitudenverlauf bezeichnet, die also durch eine Sinus-, bzw. Cosinusfunktion darstellbar ist.
x = Zustandsgröße
t = Zeit
x(t) = Zustandsgröße x zum Zeitpunkt t
y = Amplitude
ω = Kreisfrequenz
t = Zeit
Harmonische Schwingung lassen sich über die Kreisbewegung auch mit dem Phasenwinkel φ darstellen.

φ = Phasenwinkel [rad]
ω = Kreisfrequenz [s-1]
t = Zeit [s]
Gedämpfte & ungedämpfte Schwingung
Bei schwingfähigen Systemen werden gedämpfte und ungedämpfte Schwingungen unterschieden.
In einem theoretisch verlustfreien LC-Schwingkreis würde sich der Lade- und Entladevorgang zwischen Kondensator (Kapazität C) und Spule(Induktivität L) als ungedämpfte Schwingung unaufhörlich wiederholen.

Da in einer Schaltung aber Verluste auftreten (z.B. Wärmeverluste: ohmscher Widerstand R), klingt die Schwingung bei jedem Pendelvorgang allmählich ab.
Will man das Abklingen verhindern, also eine ungedämpfte Schwingung erreichen, muß man im richtigen Moment der Schwingung Energie zuführen.
Die Eigenkreisfrequenz ω0 oder Kennkreisfrequenz ω0 beschreibt das ungedämpfte System.
Die Kreisfrequenz ω beschreibt die gedämpfte Schwingung.
Zwischen der Kreisfrequenz ω und der Eigenkreisfrequenz ω0 besteht der folgende Zusammenhang:
ω = Kreisfrequenz [s-1]
ω0 = Eigenkreisfrequenz [s-1]
δ = Abklingkonstante [s-1]
Die Kreisfrequenz ω bleibt sowohl bei einer gedämpften als auch ungedämpften Schwingung während des gesamten Schwingungsvorgangs konstant.
Lediglich die Amplitude y der gedämpften Schwingung verringert sich mit zunehmender Schwingungsdauer.

Bei der ungedämpften Schwingung bleibt die Gesamtenergie des Systems erhalten. Das wird dadurch erreicht, dass einem Oszillator durch äußere Erregung eine Schwingung aufgezwungen wird.