Reflexionsfaktor Γ
Reflexionskoeffizient
Der Reflexionsfaktor Γ (≙ Reflexionskoeffizient r ) ist definiert als das Verhältnis aus rücklaufender Spannung U⇤ zur hinlaufenden Spannung U↦.
Reflexionsfaktor:
Γ = Reflexionsfaktor [1]
U⇤ = Spannung (rücklaufend) [V]
U↦ = Spannung (hinlaufend) [V]
I⇤ = Strom (rücklaufend) [A]
I↦ = Strom (hinlaufend) [A]
P⇤ = Leistung (rücklaufend) [W]
P↦ = Leistung (hinlaufend) [W]
ZV = Lastimpedanz [Ω]
ZW = Wellenwiderstand (1,2 vor/nach der Schnittstelle) [Ω]
s = Stehwellenverhältnis [1]
Der Reflexionsfaktor Γ ist ein dimensionsloser Faktor n der die Größe der reflektierten Welle im Verhältnis zur ausgehenden Welle anzeigt.
Der Reflexionsfaktor Γ ist über das Verhältnis aus Spannung (rücklaufend) U⇤ zur Spannung (hinlaufend) U↦ definiert. Er lässt sich aber auch aus der Leistung P oder aus dem Wellenwiderstand ZW und der Lastimpedanz ZV darstellen.
Ursachen der Reflexion können u.a. Steckverbindungen oder angeschlossene Kabel, Antennen und Geräte mit verschiedenen Wellenwiderständen sein.
Reflexionen entstehen aber auch durch die Leitungsgeometrie oder Isolatoreigenschaften verändernde Störstellen.
Am Leitungseingang & -ende addieren sich die vor- und rücklaufenden Spannungen U. Die Ströme I ergeben aufgrund der Phasenverschiebung am Leitungseingang einen kleineren Gesamtstrom.
Reflexionsfaktor:
Der Reflexionsfaktor Γ (Betrag) lässt sich auch aus dem Stehwellenverhältnis s errechnen:
Γ = Reflexionsfaktor [1]
s = Stehwellenverhältnis [1]
|
Für eine rein ohmsche Lastimpedanz ZV (ZV ≙ Ra) kann der Reflexionsfaktor Γ Werte zwischen -1 und +1 annehmen.
|
|||
| Reflexionsfaktor Γ | Lastimpedanz ZV | ||
|---|---|---|---|
| Γ = -1 | Kurzschluss | rücklaufende Welle um 180° phasenverschoben mit hinlaufender Welle |
ZV = 0 |
|
Verteilung von Spannung U und Strom I auf einem Antennenkabel bei Kurzschluss 
|
|||
| Γ = 0 | Anpassung | keine reflektierte Welle |
ZV = ZW |
|
Verteilung von Spannung U und Strom I auf einem Antennenkabel bei Leistungsanpassung Ri = Ra 
|
|||
| Γ = 1 | Leerlauf | rücklaufende Welle in Phase mit hinlaufender Welle |
ZV = ∞ |
|
Verteilung von Spannung U und Strom I auf einem Antennenkabel bei Leerlauf 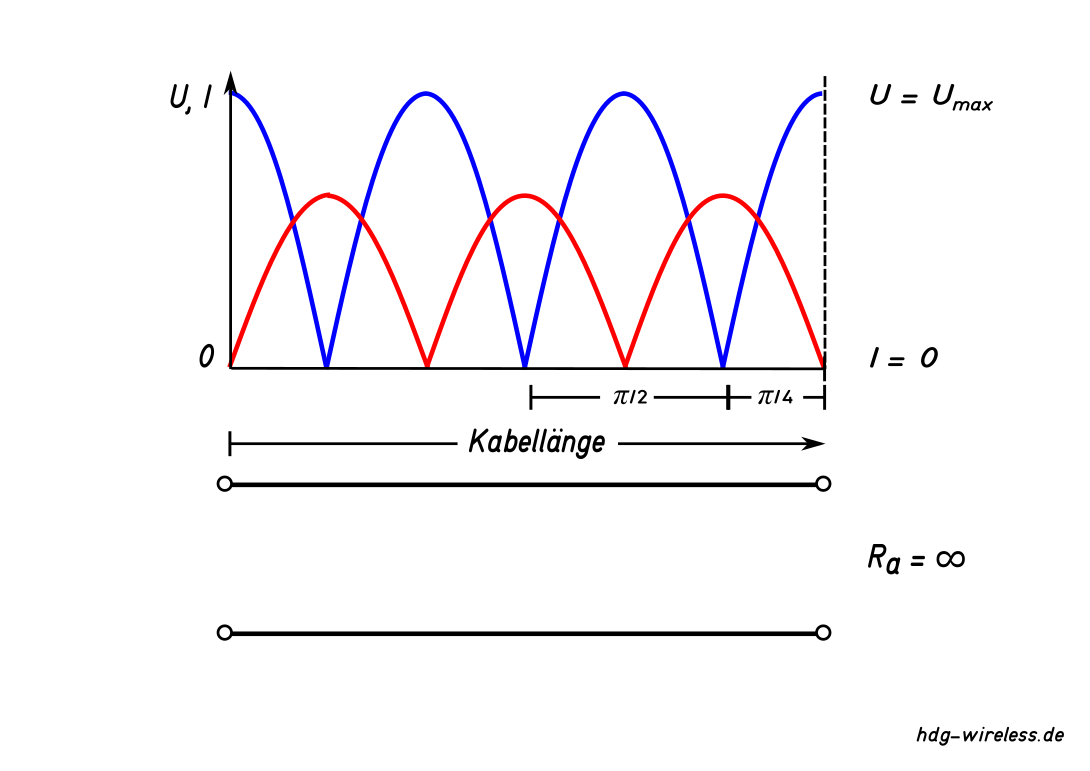
|
|||
| ZV | ZW | Reflexionsfaktor Γ | RL | αΓ | % | |
|---|---|---|---|---|---|---|
| 0 Ω | 50 Ω | -1 | Kurzschluß | 1 | 0 dB | -100% |
| 25 Ω | 50 Ω | -0.33 | Fehlanpassung | 9.18 | 9.63 dB | -11% |
| 50 Ω | 50 Ω | 0 | Anpassung | ∞ | ∞ | 0% |
| 75 Ω | 50 Ω | 0.2 | Fehlanpassung | 25 | 13.98 dB | -4% |
| 100 Ω | 50 Ω | 0.33 | Fehlanpassung | 9.18 | 9.63 dB | -11% |
| ∞ Ω | 50 Ω | 1 | Leerlauf | 1 | 0 dB | -100% |
| 0 Ω | 75 Ω | -1 | Kurzschluß | 1 | 0 dB | -100% |
| 25 Ω | 75 Ω | -0.5 | Fehlanpassung | 4 | 6.02 dB | -25% |
| 50 Ω | 75 Ω | -0.2 | Fehlanpassung | 25 | 13.98 dB | -4% |
| 75 Ω | 75 Ω | 0 | Anpassung | ∞ | ∞ | 0% |
| 100 Ω | 75 Ω | 0.14 | Fehlanpassung | 51.02 | 17.08 dB | -2% |
| ∞ Ω | 75 Ω | 1 | Leerlauf | 1 | 0 dB | -100% |
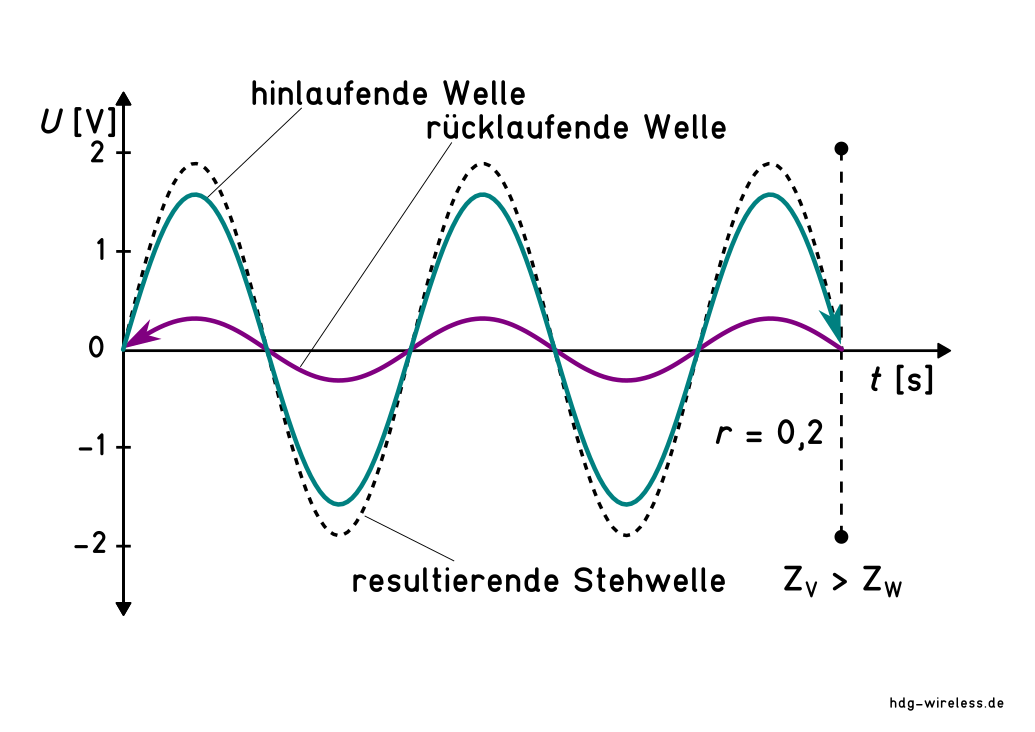
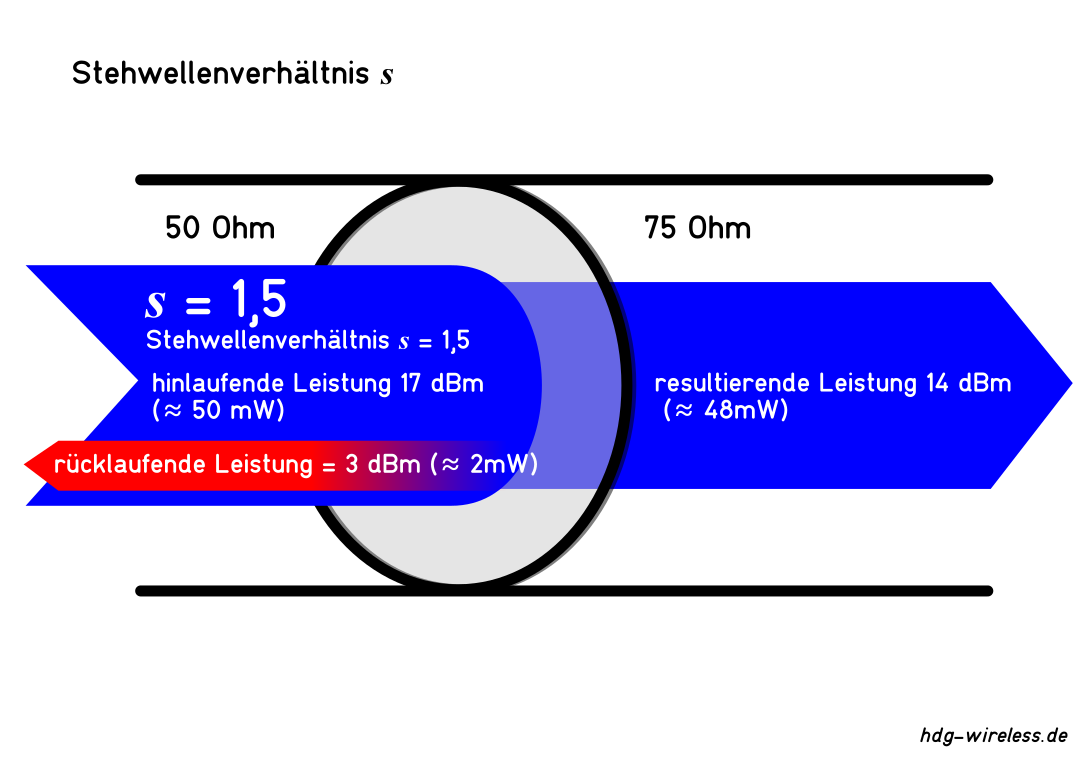
Bei Fehlanpassung einer Signalkette, z.B. wenn an einen 50 Ω - Sender ein 75 Ω - Videokabel angeschlossen wird, beträgt der Reflexionsfaktor Γ an der ersten Schnittstelle 0,2.
Γ = Reflexionsfaktor [1]
ZV = Lastimpedanz [Ω]
ZW = Wellenwiderstand [Ω]
Das bedeutet, dass die Amplitude y der rücklaufenden Welle 20 % der vorlaufenden Welle beträgt.
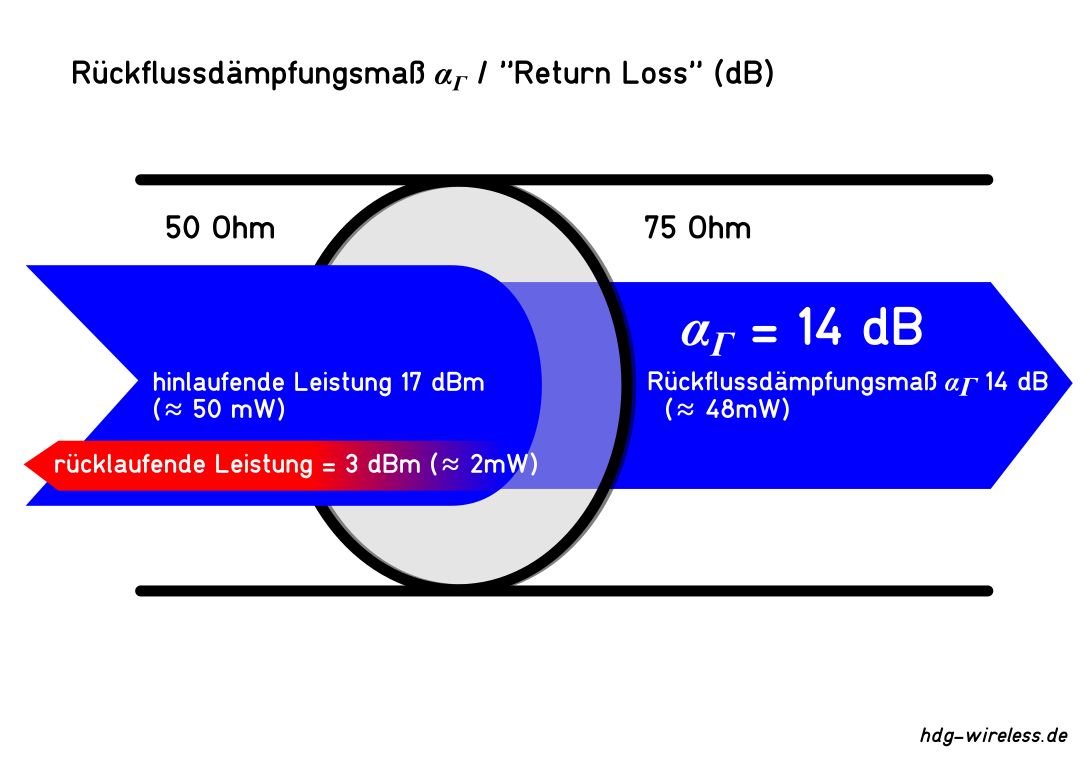
Das Rückflussdämpfungsmaß αΓ beträgt ca. 14 dB.
αΓ = Rückflussdämpfungsmaß [dB]
Γ = Reflexionsfaktor [1]
Für eine Senderausgangsleistung PA von 50 mW (ca. 17 dBm) bedeutet das eine Rücklaufleistung P⇤ von ca. 2 mW ...
17 dBm(≈ 50 mW) - 14 dB = 3 dBm (≈ 2 mW)
P⇤⇤(dBm) = Rücklaufleistung [dBm]
P⇤(mW) = Rücklaufleistung [mW]
PA(mW) = Senderausgangsleistung (mW) [mW]
αΓ = Rückflussdämpfungsmaß [dB]
Γ = Reflexionsfaktor [1]
... und eine daraus resultierende Vorlaufleistung P↦ von 48 mW die an der zweiten Schnittstelle weitergegeben werden kann.
P↦ = Vorlaufleistung [W]
PA = Senderausgangsleistung [W]
P⇤ = Rücklaufleistung [W]
Für die folgende Schnittstelle: 75 Ω - Videokabel ⇔ 50 Ω - Antenne beträgt der Reflexionsfaktor Γ dann -0,2 und somit das Rückflussdämpfungsmaß αΓ ebenfalls ca. 14 dB und die Rücklaufleistung P⇤ wiederum (etwas weniger) als 2 mW.
In der Gesamtbilanz der Verwendung eines fehlangepassten Kabels kommt ein Leistungsverlust von 4 mW, ca. 8 %, zum Tragen.

Reflexionsfaktor Γ ⇄ Rückflussdämpfungsfaktor RL ⇄ Stehwellenverhältnis s
Reflexionsfaktor Γ:
Der Reflexionsfaktor Γ (≙ Reflexionskoeffizient r ) ist definiert als das Verhältnis aus rücklaufender Spannung U⇤ zur hinlaufenden Spannung U↦.
Γ = Reflexionsfaktor [1]
U⇤ = Spannung (rücklaufend) [V]
U↦ = Spannung (hinlaufend) [V]
I⇤ = Strom (rücklaufend) [A]
I↦ = Strom (hinlaufend) [A]
P⇤ = Leistung (rücklaufend) [W]
P↦ = Leistung (hinlaufend) [W]
ZV = Lastimpedanz [Ω]
ZW = Wellenwiderstand (1,2 vor/nach der Schnittstelle) [Ω]
s = Stehwellenverhältnis [1]

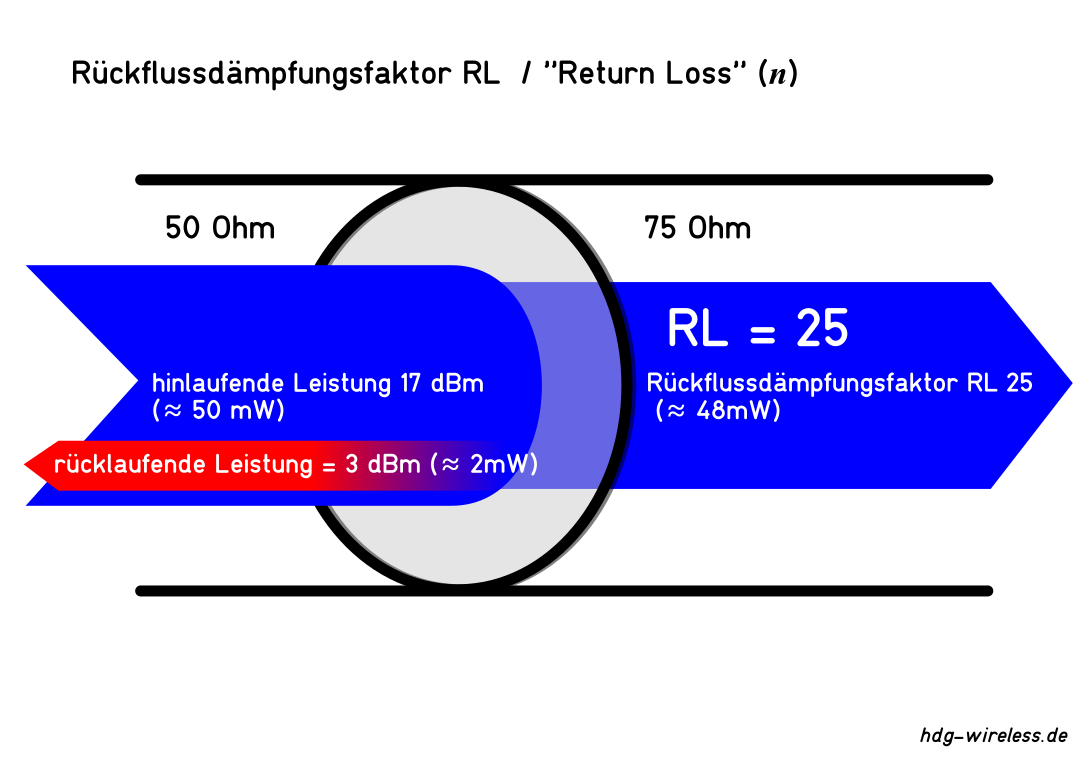
Rückflussdämpfungsfaktor RL:
Der Rückflussdämpfungsfaktor RL beschreibt das Verhältnis von hinlaufender Leistung P↦ zu rücklaufender Leistung P⇤ in einem Antennenkabel oder HF-System.
RL = Rückflussdämpfungsfaktor (Return Loss) [1]
P↦ = Leistung "hinlaufend" [W]
P⇤ = Leistung "rücklaufend" [W]
U↦ = Spannung (hinlaufend) [V]
U⇤ = Spannung (rücklaufend) [V]
Γ = Reflexionsfaktor [1]
Rückflussdämpfungsmaß αΓ:
Das Rückflussdämpfungsmaß αΓ ist der logarithmierte Rückflussdämpfungsfaktor RL und beschreibt das Verhältnis von hinlaufender Leistung P↦ zur rücklaufenden Leistung P⇤ in einem Antennenkabel.
αΓ = Rückflussdämpfungsmaß [dB]
P↦ = hinlaufende Leistung [W]
P⇤ = rücklaufende Leistung [W]
RL = Rückflussdämpfungsfaktor (Return Loss) [1]
Γ = Reflexionsfaktor [1]
Stehwellenverhältnis s:
Das Stehwellenverhältnis s ist definiert als das Verhältnis von Spannungsmaximum Umax zu Spannungsminimum Umin.
s = Stehwellenverhältnis [1]
Umax = Spannungsmaximum [V]
Umin = Spannungsminimum [V]
Γ = Reflexionsfaktor [1]
⇒ Anpassung
⇒ Impedanz
⇒ Rückflußdämpfung
⇒ Rückflußdämpfung [ ⇒Rückflußdämpfungsmaß ]
⇒ Rückflußdämpfungsfaktor
⇒ Rückflußdämpfungsmaß
⇒ Rücklaufleistung
⇒ Senderausgangsleistung [ ⇒Sendeleistung ]
⇒ Spannung
⇒ Stehwellenverhältnis
⇒ Strom
⇒ Vorlaufleistung