Komplexe Zahlen z
Eine komplexe Zahl z ist immer eine aus zwei Teilen zusammengesetzte Zahl, die auf diesen Seiten in Form des komplexen Widerstands Z vorkommt.
Als Summe definiert, stellt es sich (vereinfacht) wie folgt dar:
Der reale Anteil (bzw. die reale Zahl) der Summe ist eine reelle Zahl und wird Realteil Re(Z) genannt.
Der imaginäre Anteil (bzw. die imaginäre Zahl) ist das Produkt aus dem Imaginärteil Im(Z), ebenfalls eine reelle Zahl, und der imaginären Einheit i.Komplexe Zahlen:
z = Re(Z) + Im(Z)i
Zahl = Realteil + Imaginärteil · imaginäre Einheit
z = komplexe Zahl [1]
Re(Z) = Realteil [Ω]
Im(Z) = Imaginärteil [Ω]
i = imaginäre Einheit
Eine reelle Zahl x kann nach dieser Definition als komplexe Zahl z dargestellt werden:
Der Imaginärteil Im(Z) einer komplexen Zahl z ist die (reelle) Zahl vor der imaginären Einheit i, also der Faktor mit dem die imaginäre Einheit i multipliziert wird.
Die imaginäre Einheit i, j ist per Definition eine Zahl, deren Quadrat gleich -1 ist.
i und -i sind komplexe Zahlen, deren Realteil gleich null ist. φ∠(i, -i) = 180°
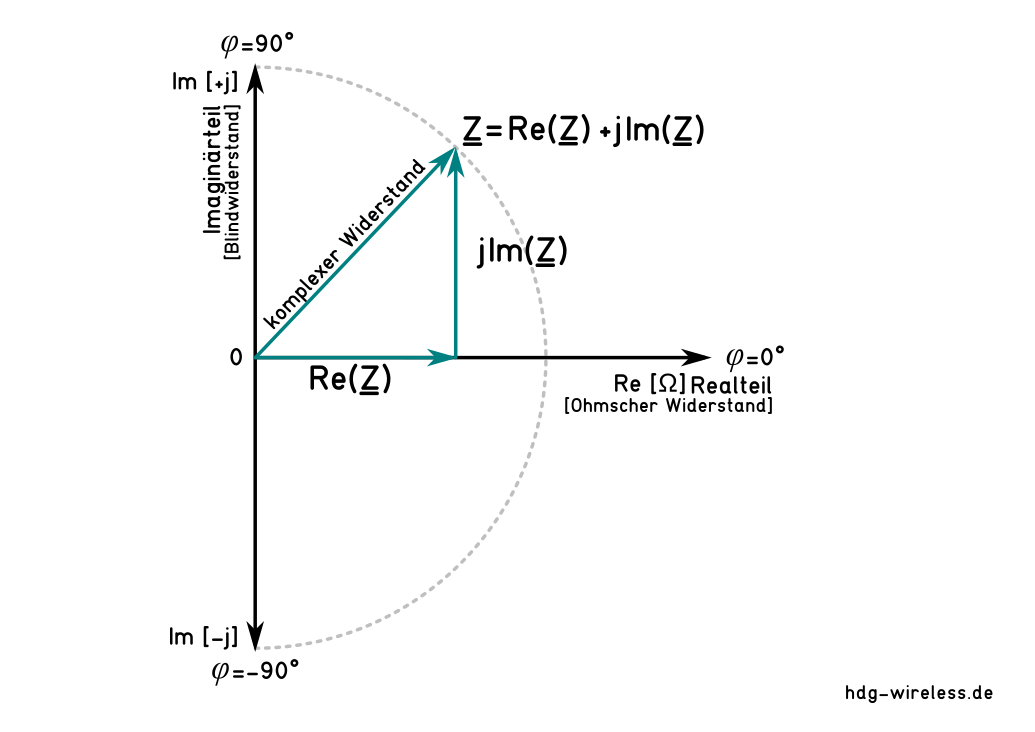
⇒ Blindwiderstand
Formelsammlung
⇒ Imaginärteil
⇒ Impedanz
⇒ Komplexer Widerstand
⇒ Ohmscher Widerstand
⇒ Realteil
⇒ Scheinwiderstand
⇒ Wechselstromwiderstand [ ⇒Komplexer Widerstand ]