Impedanz Z
Wechselstromwiderstand, Wellenwiderstand
Die Impedanz Z ist ein Sammelbegriff und beschreibt die hemmende Wirkung auf unterschiedliche physikalische Wechselgrößen aufgrund ihrer elektrischen und magnetischen Eigenschaften und deren Wechselwirkung auf das sie umgebende Medium.
Auf diesen Seiten kommen im Wesentlichen die folgenden Impedanzen Z vor[1]:
→ elektrische Impedanz Z [2]
- komplexe Impedanz Z
- komplexer Widerstand Z
- Scheinwiderstand |Z|
- Wechselstromwiderstand Z
→ Wellenimpedanz ZW [2]
- Strahlungsimpedanz
- Eingangsimpedanz ZE
- Fußpunktwiderstand ZE
- Antennenimpedanz ZA
- Leitungswellenwiderstand ZL
- Kabelimpedanz ZL
- Wellenwiderstand ZW
- Freiraumwellenwiderstand Z0
- Feldwellenwiderstand ZF
[1] Diese Liste hat keinen Anspruch auf Vollständigkeit.
[2] Die folgenden Begriffe sind teilweise synonym oder kommen im Kontext der jeweiligen Impedanz Z vor.
Auffällig ist die umgangssprachliche Vermischung der Begriffe Impedanz und Widerstand.
Um die Begriffe nochmal grundsätzlich voneinander abzugrenzen werden in dieser Rubrik (hier) die Unterschiede nur kurz abgehandelt. Detailliertere Informationen finden sich in den entsprechenden Rubriken dieses Glossars.
Mit Widerstand wird i.d.R. der rein ohmsche Widerstand R bezeichnet.
Der ohmsche Widerstand R kommt sowohl bei Gleichstrom⎓ als auch bei Wechselstrom ≂ vor und begrenzt den Stromfluss.
Dabei wird die elektrische Energie im Widerstand in Wärme umgewandelt (≙ Wirkwiderstand R).
Das Verhältnis aus der anliegenden elektrischen Spannung U zur Stromstärke I bleibt dabei gleich, d.h. eine Erhöhung der Spannung U erhöht auch den elektrischen Strom I und umgekehrt.
Mit Impedanz wird in der Elektrotechnik die komplexe Impedanz Z (≙ komplexer Widerstand Z), bzw. in der Wellenausbreitung die Wellenimpedanz ZW (≙ Wellenwiderstand ZW) bezeichnet.
komplexer Widerstand Z:
Die komplexe Impedanz Z läßt sich sowohl als Summe aus Wirkwiderstand R und Blindwiderstand X mit der imaginären Einheit j darstellen als auch als Produkt aus dem Betrag des komplexen Widerstands Z (≙ Scheinwiderstand |Z|) und dem Phasenwinkel φ.
Z = komplexer Widerstand [Ω]
R = Wirkwiderstand (ohmscher Widerstand) [Ω]
X = Blindwiderstand [Ω]
φ = Phasenwinkel [rad]
Der Unterstrich der komplexen Impedanz Z verweist auf den mathematischen Begriff der komplexen Zahlen z und deren Eigenschaften.
Wellenwiderstand ZW:
Je nach dem betrachteten Medium kann zwischen Freiraumwellenwiderstand Z0, Feldwellenwiderstand ZF oder Leitungswellenwiderstand ZL unterschieden werden.
In homogenen, isotropen Ausbreitungsmedien (z.B. Vakuum, Luft) ist der Feldwellenwiderstand ZF das Verhältnis aus der elektrischen Feldstärke E zur magnetischen Feldstärke H.
ZF = Feldwellenwiderstand [Ω]
E = elektrische Feldstärke [Vm-1]
H = magnetische Feldstärke [Am-1]
µ = Permeabilität [Hm-1]
ε = Permittivität [Fm-1]
µ0 = Magnetische Feldkonstante [NA-2]
ε0 = Elektrische Feldkonstante [Fm-1]
εr = Relative Permittivität [1]
µr = Relative Permeabilität [1]
Z0 = Freiraumwellenwiderstand [Ω]
j = imaginäre Einheit [1]
ω = Kreisfrequenz [s-1]
σ = elektrische Leitfähigkeit [Sm-1]
Der Freiraumwellenwiderstand Z0 stellt dabei eine Sonderform des Feldwellenwiderstand ZF dar und ist eine Naturkonstante.
Z0 = Freiraumwellenwiderstand [Ω]
µ0 = Magnetische Feldkonstante [NA-2]
ε0 = Elektrische Feldkonstante [Fm-1]
c0 = Lichtgeschwindigkeit im freien Raum [ms-1]
In einem längshomogenen Ausbreitungsmedium (z.B. Leitung) ist der Leitungswellenwiderstand ZL das Verhältnis aus Induktivitätsbelag L' zum Kapazitätsbelag C', bzw. dem Verhältnis aus Freiraumwellenwiderstand Z0 und der relativen Permittivität εr des Dielektrikums in Abhängigkeit von der Geometrie des Leiterquerschnitts.
ZL(Koax) = Leitungswellenwiderstand Koaxialkabel [Ω]
L' = Induktivitätsbelag [Hm-1]
C' = Kapazitätsbelag [Fm-1]
R' = Widerstandsbelag [Ωm-1]
G' = Ableitungsbelag [Sm-1]
j = imaginäre Einheit [1]
ω = Kreisfrequenz [s-1]
π = Kreiszahl (Pi) [1]
Z0 = Freiraumwellenwiderstand [Ω]
εr = Relative Permittivität [1]
D = Aussendurchmesser [m]
d = Innendurchmesser [m]
Wichtige Übereinstimmung aller hier beschriebenen Impedanzen Z sind:
- Impedanzen Z treten bei physikalische Wechselgrößen auf.
- die Wechselgrößen weisen elektrische und magnetische Eigenschaften auf und deren Wechselwirkung mit den elektrischen und magnetischen Eigenschaften des sie umgebenden Mediums wirkt sich hemmend auf deren Ausbreitungseingenschaften aus.
Für die komplexe Impedanz Z in der Elektrotechnik gilt, dass wenn sich die induktiven und kapazitiven Anteile des Blindwiderstands X einer elektrischen Schaltung ausgleichen, wirkt nur der rein ohmsche Widerstand R (≙ Wirkwiderstand R).
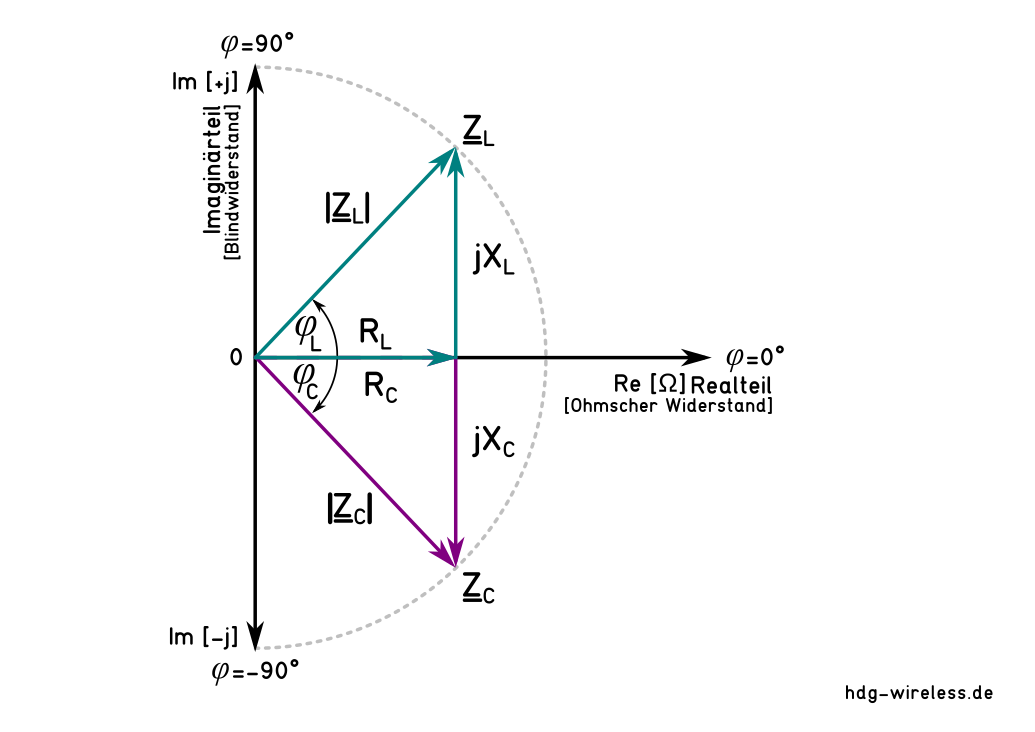
Für die Wellenimpedanz ZW bei der Ausbreitung einer elektromagnetischen Welle gilt, dass die (elektrische) Permittivität ε und die (magnetische) Permeabilität µ des umgebenden Mediums sich hemmend auf die Ausbreitung der Welle auswirkt, ebenfalls aufgrund ihrer elektromagnetischen Eigenschaften.